De o buna bucata de vreme ma chinuie o idee. Am incercat sa demonstrez/calculez singur daca ideea functioneaza sau nu, dar n-am reusit.
Calculele imi indica ca sistemul ar functiona si inca foarte bine. Ceea ce nu pusca cu ceea ce estimam inainte de calcule. Asta imi sugereaza ca e foarte posibil sa existe undeva cel putin o greseala.
Am apelat la cateva persoane cu mai multe cunostinte in fizica decat mine, dar tot n-am reusit sa ajungem la o concluzie.
Deci, va pun la dispozitie ideea, explicatiile, calculele, si va rog, cine stie si poate, sa verifice atat conceptul cat si calculele si sa imi arate/demonstreze ca acest concept fie nu functioneaza, fie functioneaza, iar daca sunt greseli, care sunt ele, unde sunt si de ce, ca sa pricep si eu.
Va rog, nu faceti paralele cu alte sisteme. Sa concluzionezi ca acest sistem nu functioneaza pt ca se aseamana cu un pendul sau biela-manivela sau mai stiu eu ce, este total gresit. Si un triunghi metalic se asemana cu un triunghi la fel de mare si gros, dar de lemn, dar unul arde la 180 de grade, allant la 1000+ in functie de ce e in el. Unul conduce electricitatea mai bine ca allant samd.
Deci, adopdati rabdare, citit totul cu atentie, nu sariti peste idei si incercati sa priviti lucrurile fara prejudecati. Eu am incercat sa prezint lucrurile intr-o ordine logica a proceselor si am incercat sa explic pe cat pot eu de bine cum ar trebui (cum ma astept) sa functioneaza treaba, sper ca e totul clar. Daca aveti intrebari, puneti, o sa incerc sa raspund, in limita a ceea ce stiu.
Daca e cineva cu ceva cunostiinte grafice sa faca o animatie a procesului, ceva basic, e binevenit.
Simplificare sub-sistemului de pompe se poate reprezenta ca mai jos
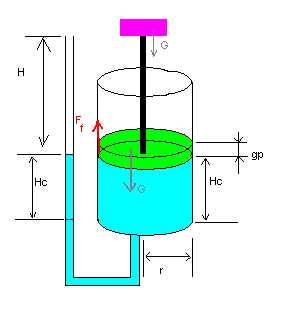
unde corpul roz/mov de greutate G reprezinta practic apa din colectorulA, scurs deasupra pistonului.
In figura de mai sus, analizand principiul de functionare observam ca, la inceputul fiecarui ciclu, pt acelasi G fixat si suficient de mare, pistonul va ridica aceasi cantitate de apa din cilindru prin coloana de apa din furtun la inaltimea H in acelasi timp TT (unde acesta se va scurge in colectorul A).
Intrucat se mentin cantitatile de apa constante la fiecare pas (raportate la cilcu), rezulta ca si fortele de reactiune vor fi aceleasi, deci si energia utila rezultata per ciclu va fi aceeasi.
Cheia sistemului consta exact in mentinerea cantitatilor de apa din colectoare si cilinidri la fiecare pas si per ciclu, acest lucru garantand ca sistemul functioneaza pina cand o piesa din sistem se va uza suficient de mult ca sa compromita sistemul (de ex materialul (cauciucul) folosit de piston ca sa etanseizeze contactul intre peretele cilindrului si discul pistonului se va uza intr-atat incat se va fisura si deci nu va mai asigura etanseitate, astfel nu se va mai pompa aceeasi cantitate de apa in colector)
Functionare:
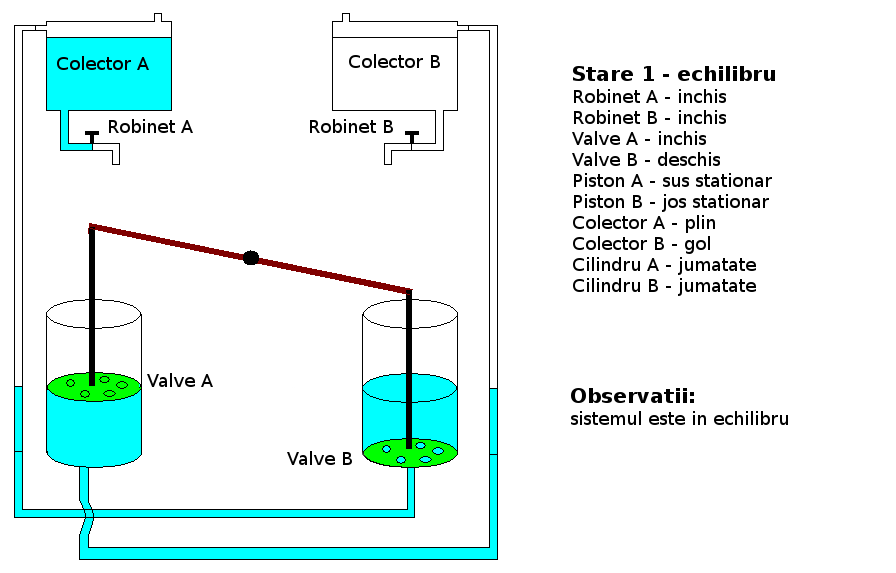
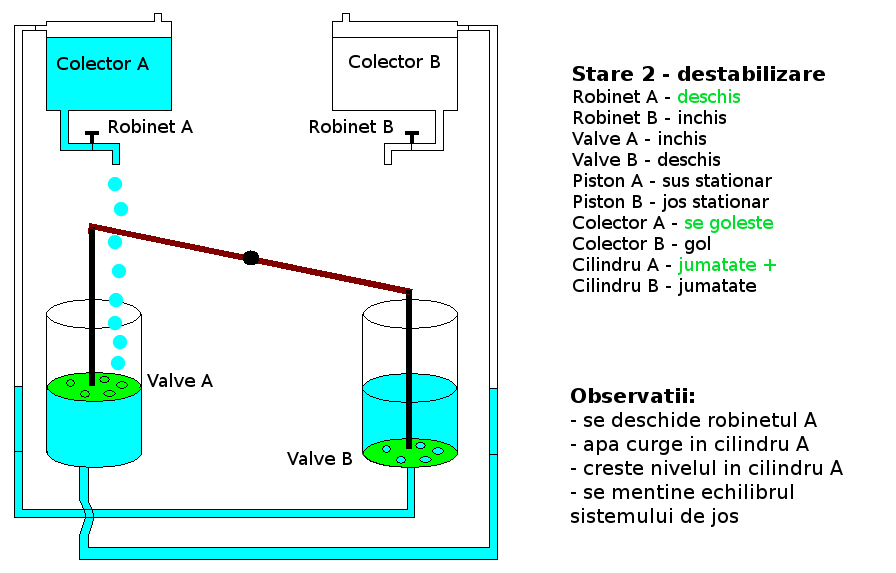
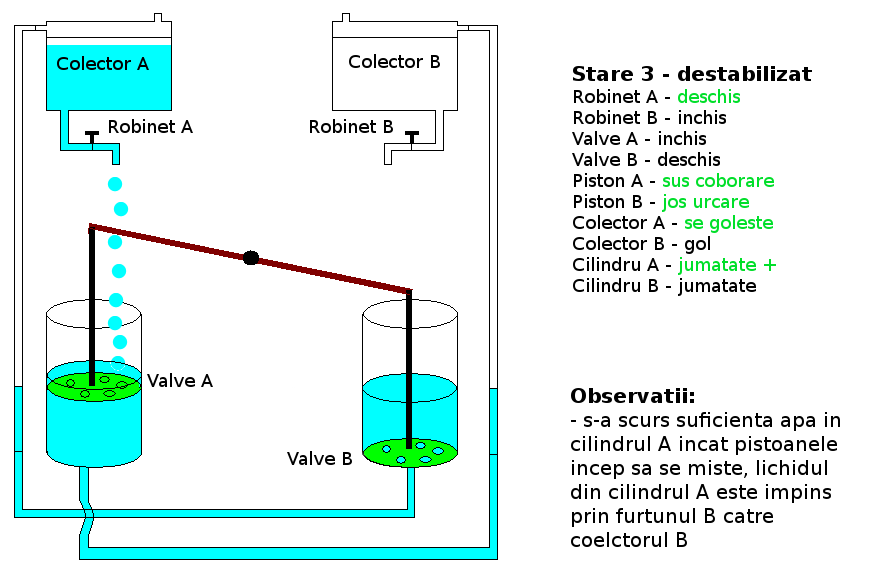
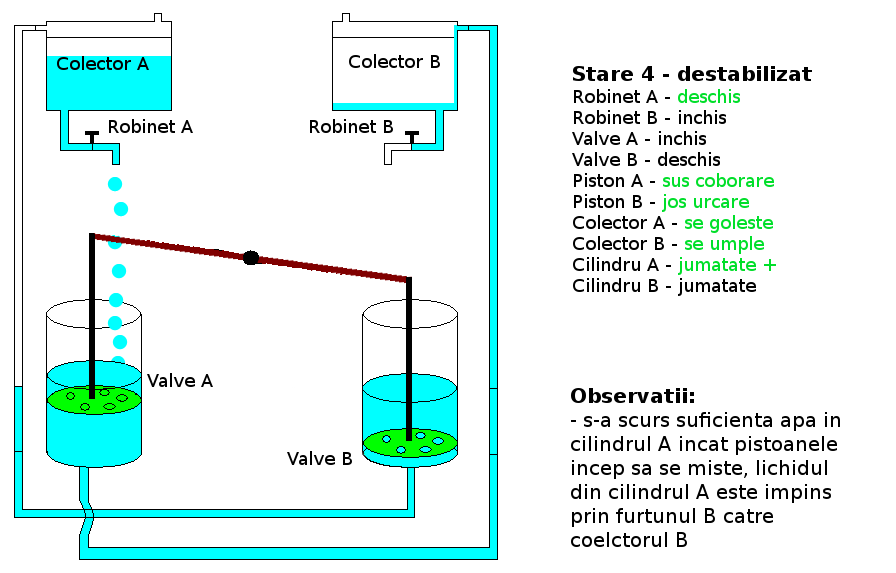
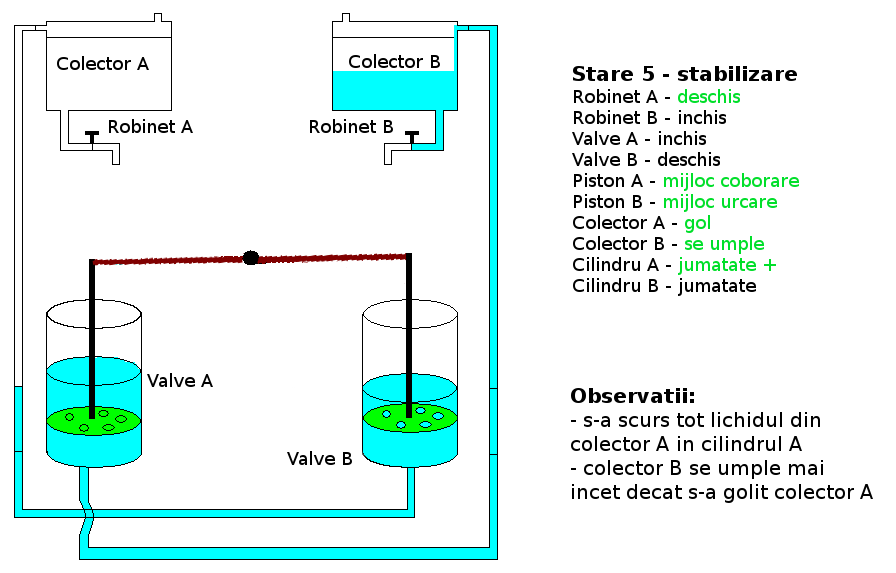

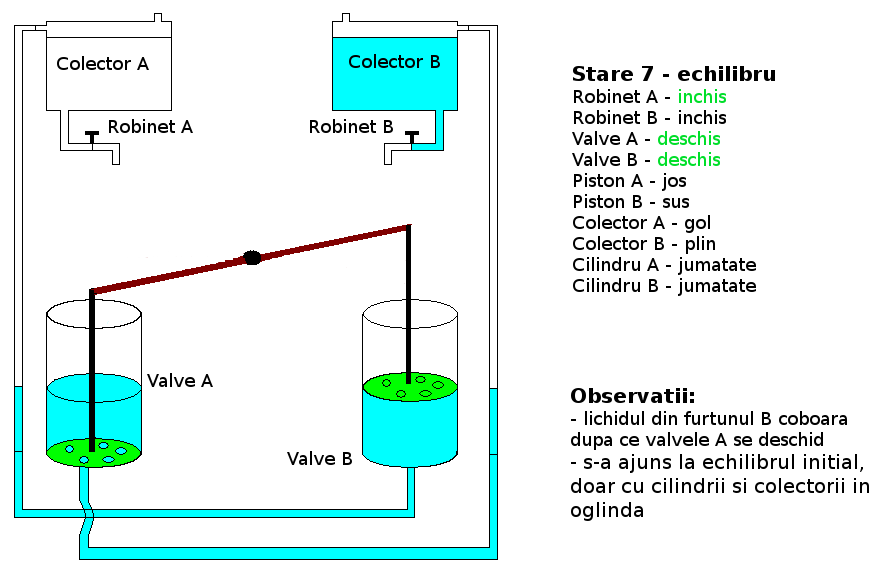
Teste:
– Am verificat o pompa de apa de copii (http://img08.mercador.ro/images_mercadorro/11808239_2_644x461_pompa-stropit-apa-cadouri-jucarii-cod-733depozit-jucarii-fotografii.jpg) model mic, masurand ce forta suporta mecanismul lui de piston. Folosind un cantar de baie, astupand gaura si impingand in jos, pompa a rezistat la 34 KG forta inainte ca discul pistonului sa se strice.
In concluzie, folosind acelasi mecanism putem implementa un sistem care sa permita cel putin 34 L apa in colectorul A.
– Am masurat cu un cantar de bagaje forta de frecare la aceeasi pompa, aceasta rezultand la aproximativ 0.5 KG forta.
Calcule:
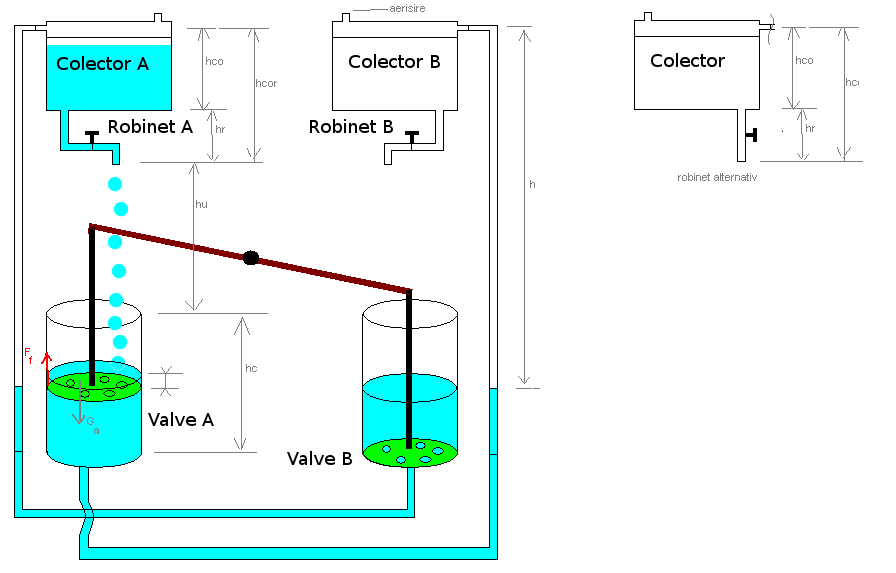
Simplificari
Intrucat sistemul presupune doua miscari (per cilindru) functie de timp, acestea vor implica diferentiale de timp si/sau distanta pentru formulele in cauza. Intrucat in acest moment incercam sa calculam/vedem daca sistemul este viabil, este suficient sa minimizam utilul si sa maximizam pierderile. Daca in aceste conditii sistemul functioneaza, atunci e clar ca si in conditiile efective, acesta va functiona, eventual chiar cu un randament mai mare.
Aceste simplificari ne ajuta sa lucram cu formule simple, mai pe intelesul publicului larg, in acelasi timp oferind formule de calcul usoare/simplificate care arata orientativ niste valori aproape de realitate, fiind si mai usor de implementat in simulatoare de exemplu (care ar trebui sa fie pasul urmator in cazul in care sistemul chiar pare sa functioneze).
Masa de apa din coloana
pt un h dat, masa apei din coloana care trebuie ridicata de piston, notata cu mh este data de formula
unde Vh este volumul coloanei, iar RO este densitatea lichidului (apei) din coloana.
Coloana fiind cilindru (furtun), volumul acesteia este dat de formula
unde Sh este suprafata sectiunii furtunului, adica
unde pi este constanta egal aprox cu 3.14 iar r2 este raza sectiunii la patrat.
Rezulta ca masa mh, pt o coloana de inaltime data h si raza interna a furtunului r este data de formula
Orientativ, pt o inaltime fixata de h = 10m, si un furtun cu diametru d = 2*r = 3 cm = 0.03m rezulta o masa a apei din coloana de aproximativ
mh = 3.14 * (0.03/2)^2 * 10 * 1000 = 7.065 kg
Masa de apa maxima pt a ridica apa mh in coloana
Pentru a calcula forta necesara ridicari unei coloane de apa in conditiile de mai sus, vom folosi egalitatea de forte in sistemul din poza, si anume:
avand in vedere conditiile de lucru (cantitati consistente, furtun NE-capilar, etc), consideram forta de frecare a apei prin furtun ca fiind neglijabila (egala cu 0).
– Ga este forta de greutate maxima a apei care actioneaza asupra pistonului astfel incat apa se ridica in coloana la inaltimea h+x, dar nu mai mult. Orice forta mai mare, va pune pistonul in miscare
– Ff este forta de frecare dintre discul pistonului si peretele cilindrului
– Gh este forta de greutate a apei din coloana
– x este distanta parcursa de piston in jos pt a disloca o cantiate de apa suficienta pentru a umple furtunul pina la inaltimea h
Ff este constanta cat timp pistonul se afla in miscare
– ma este masa apei care actioneaza asupra pistonului
– mh este masa din coloana calculata la inceput
– g este aceleratia gravitationala
Deoarece este necesar sa se umple furtunul pina la inaltimea h, rezulta ca pistonul va cobora o distanta x, iar in final, pistonul va mentine o coloana de apa egala cu h+x.
Deoarece lucram cu o inaltime h relativ mica, g va fi practic constanta pe toata inaltimea coloanei. Chiar si pt o inaltime mai practica in instalatiile hidrocentrale in cadere de h = 100m, valoarea acceleratiei gravitationale tot nu variaza considerabil, cat sa conteze.
Tinem cont de faptul ca pistoanele se afla intr-o relatie de “balanta”, deci greutatea discului si a pistonului devine aproape neglijabila in conditiile unui hc (inaltime a cilindrului) relativ mic (ceea ce probabil se va intampla in practica pt a mari hu (inaltimea utila), vezi detaliile mai jos)
Pentru usurarea calculelor, vom exprima forta de frecare Ff ca fiind egala cu forta de greutate al unei mase de apa mf. In acest sens, vom avea
si tinem cont ca mf este constant, iar daca luam in considerare valoarea din teste, avem mf = 0.5 kg.
adica, pentru mh calculat mai sus de 7.065 kg si mf masurat in teste de 0.5 kg, avem o cantitate minima de apa ca sistemul sa functioneze de ma = 7.565 kg
Pentru a disloca o masa de apa de mh = 7.065 kg calculata mai sus, un piston de diametru (ales empiric) dp = 60cm = 0.6m = 2*rp avem masa apei dislocate egala cu mh deci
mh = Vx * RO
unde Vx este volumul de apa dislocat de piston, deci
mh = Sx * x * RO
de unde rezulta
x = mh / (Sx * RO)
unde Sx este aria pistonului, deci
x = mh / (pi * rp2 * RO)
iar pt
mh = pi * r2 * h * RO
rezulta
x = pi * r2 * h * RO / (pi * rp2 * RO)
adica
x = h * (r/rp)2
Orientativ, pt
h = 10m
r = 3cm = 0,03m
rp = 30cm = 0,3m
avem
x = 10 * (0,03/0,3)^2 = 0.1m = 10 cm
Deci in practica, comparativ cu h > 10m, x-ul este neglijabil. Il vom considera deci ca parte a h.
Restrictii la inaltimi
Pentru ca sistemul sa functioneze, inaltimea colectorului cu furtun si robinet (hcor) plus jumatate din inlatimea cilindrului (hc) trebuie sa fie mai mica decat h. Notam aceasta diferenta de inaltime cu hu (h util).
– hco este inaltimea colectorului
– hr este inaltimea furtunului cu robinet de la colector
De retinut ca optimizarea consumului de energie ne permite, in teorie (nefind foarte practic) utilizarea unui colector de inaltime foarte mica si suprafata mare, astfel minimizand pierderea de energie in inaltime, marind hu (h util) pentru acelasi h dat.
In aceeasi idee, se pot minimiza hr, si hc.
Energiile
Avand sistemul de pompe astfel functional, calculam energiile din joc ca sa putem avea macar o idee asupra energiei consumate si generate de sistem intr-un ciclu (anume trecand din faza A in faza B, care e practic A in oglinda).
Intrucat viteza cu care apa se scurge prin robinetul A este variabila in functie de timp, deoarece depinde de presiunea apei din colectorul A, care presiune scade o data cu scurgerea apei, este clar ca si energia generata va scadea in timp, pe parcursul unui ciclu.
Pentru a usura calculele si intrucat practic este suficient sa calculam energia minima generata, consideram urmatoarele:
– apa se scurge prin robinetul A si B cu aceeasi viteza constanta, egala cu viteza minima care se produce la ultima “picatura”, adica ultima canitate de apa aflata doar pe furtunul si robinetul A/B, adica mr considerat pe un furtun cu robinet liniar de inaltime hr, ca in desen, marcat “robinet alternativ”
adica energia potentiala Ep a masei de apa mr la inaltimea hu (h util), unde
– Vr este volumul apei in furtun + robinet
– RO este densitatea apei
– Sr este suprafata sectiunii furtunului
– hr este inaltimea furtunului cu robinet
– rr este raza sectiunii interioare a furtunului
Ep = pi * rr^2 * hr * RO * g * hu
Intrucat sistemul este inchis (nu se pierde apa prin evaporare), putem considera Ep = Ec = E
Timpul de golire colector
Pentru a calcula timpul in care se goleste colectorul, vom considera aceeasi scurgere constanta ca mai sus la calculul energiei cinetice/potentiale, timpul efectiv fiind defapt mai mic.
Conform legii miscarii avem
x = x0 +v0 * (t – t0) + (a * (t – t0)^2)/2
– x0 este dinstanta initiala
– x este distanta parcursa de la x0
– t0 este momentul initial
In conditiile unei scurgeri constante/liniare, cu punctul de pornire in capatul initial al furtunului, avem
– a = g (acceleratia gravitationala)
– SQRT este functia radical
– hr este inaltimea furtunului cu robinet
– g este acceleratia gravitationala
– tr este timpul necesar unei mase mr sa se scurga prin furtunul robinet in cadere libera de lungime hr
Pentru o masa de apa totala in colector in cantitate m, timpul necesar golirii colectorului este
Puterea pe ciclu
In final, putem calcula puterea generata de sistem pe un ciclu ca fiind
P = mr * g * hu / SQRT(2 * hr / g) = pi * rr^2 * hr * RO * g * hu / SQRT(2 * hr / g)
facem un artificiu de calcul pentru simplificarea fractiei prin inmultirea cu
1 = 1/1 = SQRT(2 * hr / g) / SQRT(2 * hr / g)
P = pi * rr^2 * hr * RO * g * hu * SQRT(2 * hr / g) / (2 * hr / g)
urcam g-ul de sub fractie sus
P = pi * rr^2 * hr * RO * g^2 * hu * SQRT(2 * hr / g) / (2 * hr )
simplificam un g in radical, prin bagarea unui g sub radical ca si g^2, rezulta
P = pi * rr^2 * hr * RO * g * hu * SQRT(2 * hr * g) / (2 * hr )
simplificam un hr de sub fractie cu cel de sus
P = pi * rr^2 * RO * g * hu * SQRT(2 * hr * g) / 2
Pentru urmatoarele valori fixate (alese relativ empiric)
– rr = 3/2 cm = 1.5 cm = 0.015 m (furtun cu robinet diametru 3 cm)
P = 3.14 * 0.015^2 * 1000 * 9.8 * 8 * SQRT(2 * 0.1 * 9.8)/ 2 = 77,54544 w
(personal, valoarea asta fiind per ciclu, mi se pare enorma dar nu imi dau seama unde am gresit)
Pentru un hidro-generator electric avem randamente incepand de la 80% pina la putin peste 90%. Cum constrangerile auto-impuse ne forteaza sa calculam un minim in acest caz, vom utiliza un randament de 80%.
Astfel, puterea utila devine
Pu = P * 80% = 62,036352 w






















